CONTRIBUTORS

Whether you are burying power cables, building roads, or to simply trying to understand heat transfer or storage in the soil, there are many reasons to measure the thermal properties of a specific soil profile. Unfortunately, the ground where you need to measure is not always pristine, uniform soil. Instead, you may need to calculate the thermal conductance and resistance of a soil peppered with stones to varying degrees. How do you ensure that your calculations consider the thermal conductance of each material found within the soil profile, no matter its contents? In this article we will discuss what measurements to collect, and the calculations required to produce accurate thermal conductivity predictions in even the stoniest of soils.

To fully understand why a measurement of just the soil in a profile with significant rock presence would be inaccurate, let’s explore the conductivity of several common types of stone you may.

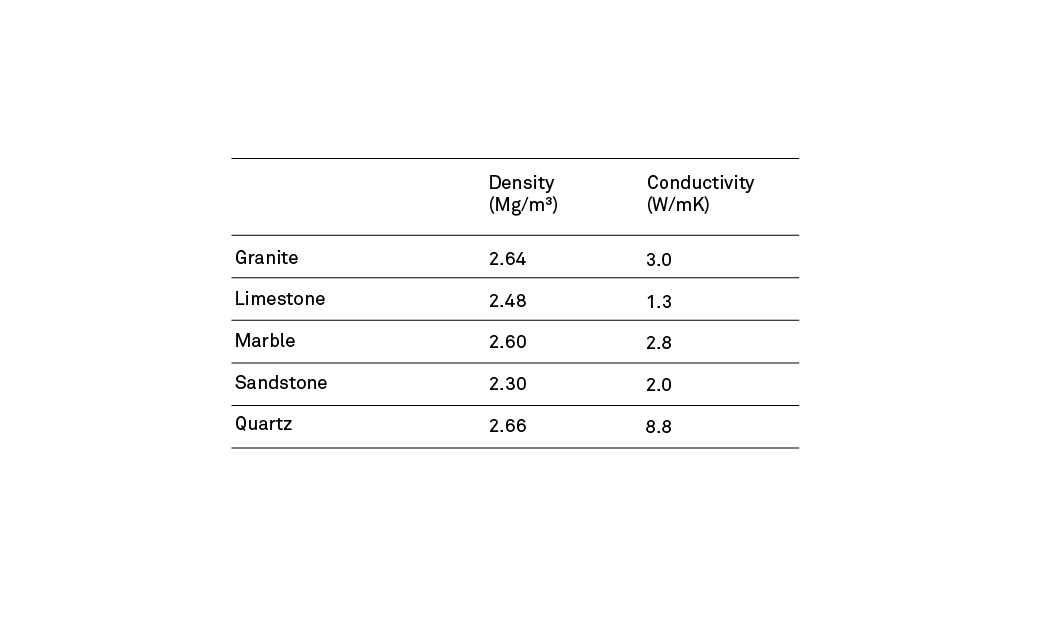
The chart in Fig 2 illustrates that even with similar densities, the conductivity of each stone type varies greatly. In addition to their density, the porosity of the rocks can change the water content, directly affecting thermal conductivity. For the purposes of this article, we will assume the conductivity of the rock can be measured and that the water content within the rock is constant.

The soil material between the rock typically has a density of about half that of the rock. Expect the thermal conductivity of the soil to vary almost at an order of magnitude from dry to wet.

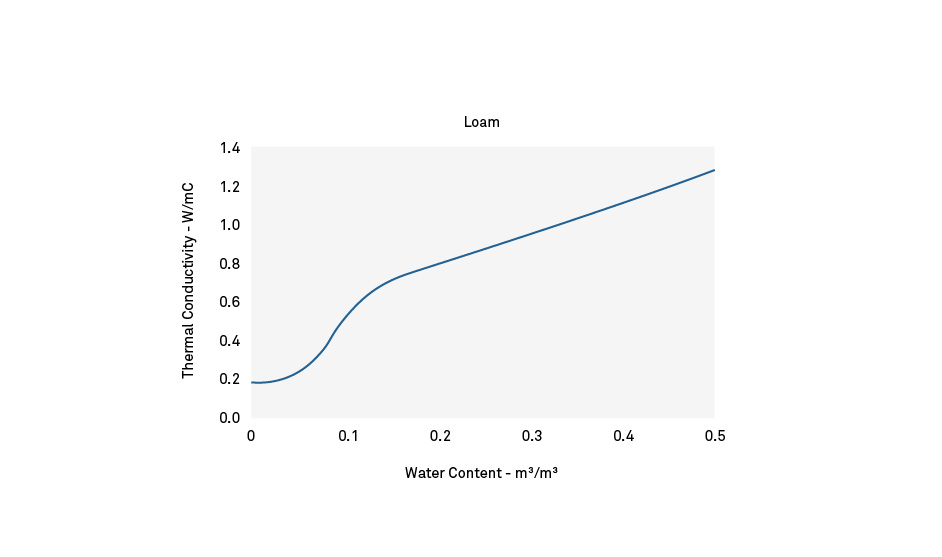
Fig. 3 shows an example of a typical relationship between thermal conductivity and water content with dry soil having a thermal conductivity of less than 0.2 W/mC and a saturated thermal conductivity of 1.2 W/mC or greater. All of these are lower than the conductivity values shown for stones in Fig. 2, and other soils have an even lower conductivity.

With all of these variables in play, how do we model the accurate thermal conductivity of stony soils? Even if you determine that an average should be calculated, you’re still left with the decision of what type of average to choose.

Parallel vs. series

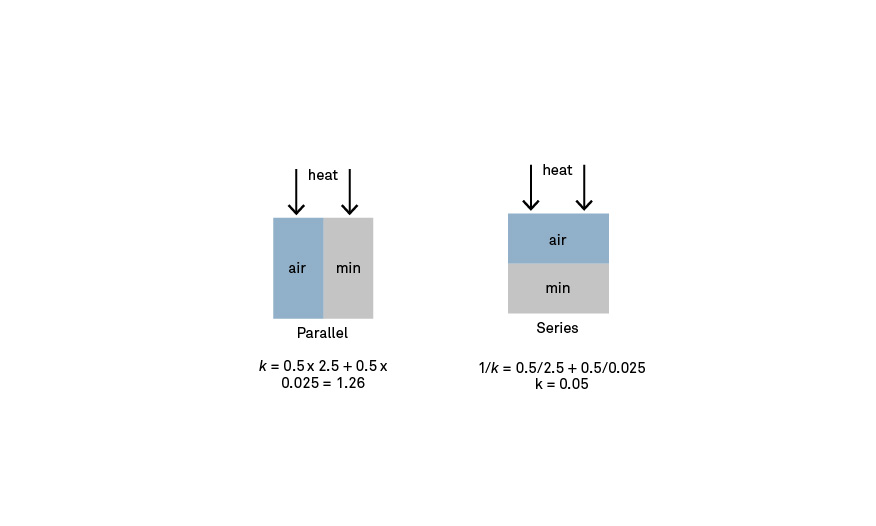
Fig. 4 shows an extreme example of the pore structures of air and marble in different configurations, assuming each takes up half of the total volume. The left side illustrates one arrangement, which has the air and marble pores in parallel to the heat source. Calculating the thermal conductivity of that system would only require a weighted arithmetic average of the two.

k = 0.5 x 2.5 + 0.5 x 0.025

k = 1.26

On the right of Fig. 4 is the system in series. This arrangement requires calculating the harmonic mean of the reciprocal of the conductivity of the mixture, which is the sum of the reciprocals of the conductivity of the components. In this configuration, the air determines the amount of heat that can flow into the marble because it acts as a barrier that all heat has to pass through before reaching the rock.

1/k = 0.5/2.5 + 0.5/0.025

k = 0.05

Any mixture of rock and soil that you come across will be somewhere between these two extremes. So how do you model mixtures in other arrangements?

The De Vries model

This problem is very similar to the problems encountered when attempting to model heat flow in other porous mediums. De Vries derived his model from a previous model of dielectric constant mixtures based on a dry sand. The original model dealt with the continuous phase of air where the spheroidal inclusions of sand were suspended. The same model can be used to measure a stony soil by changing the materials involved. In this application, the continuous phase will be soil and the spheroidal inclusions will be rock. To make these calculations, you must first know the thermal properties of the rock and soil along with their volume fractions.

Fig. 5 shows the de Vries model itself. The top equation shows that the thermal conductivity of the mixture is a weighted sum of the two components of the mixture. The second equation defines the calculation of the weight factor.

For the shape factor (g), assume the rocks are spheroids with axes a, b, and c. For these purposes, we will assume that axes a and b are the same, leaving only a and c in the equation shown in Fig. 6.

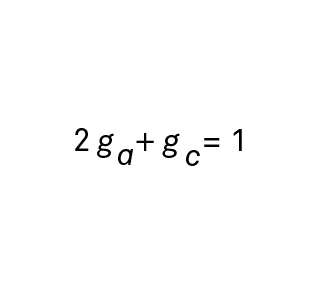
If the inclusions are spherical stones, the shape factor for all three axes will be g = 0.33. For elongated stones, g_a and g_b become smaller and g_c becomes bigger, but they will add up to 1.

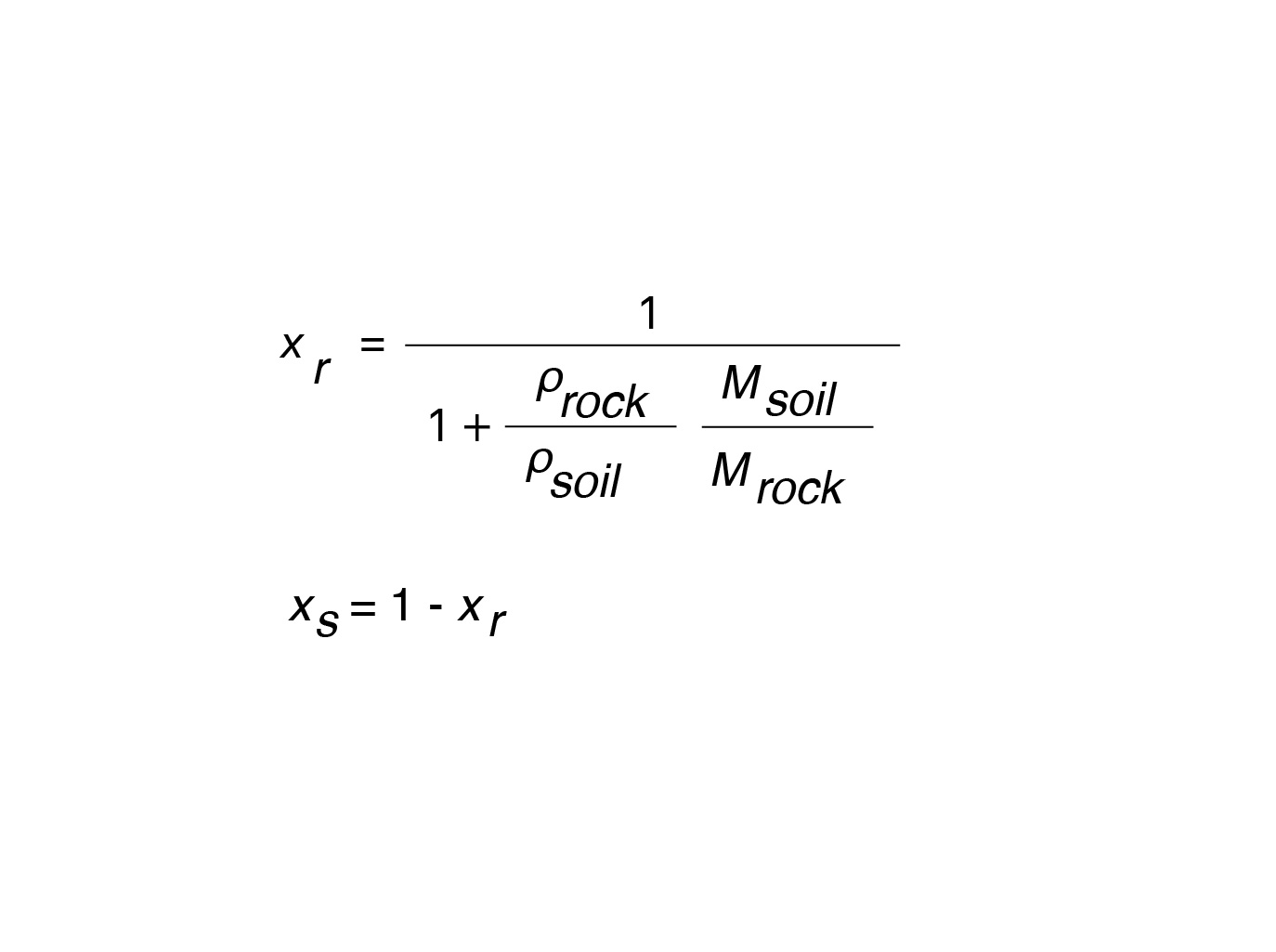
The volume of the rock and soil are best derived from the density and mass of each. The equation in Fig. 7 illustrates how the volume fractions are calculated.

Conducting measurements

The de Vries model requires several measurements to be collected before calculations can be made. Some porous rocks have water content-dependent thermal conductivity, which will need to be determined if such rocks are present in the soil you’re studying. The rock shown in Fig. 8 has very little porosity so a single value for its thermal conductivity suffices.

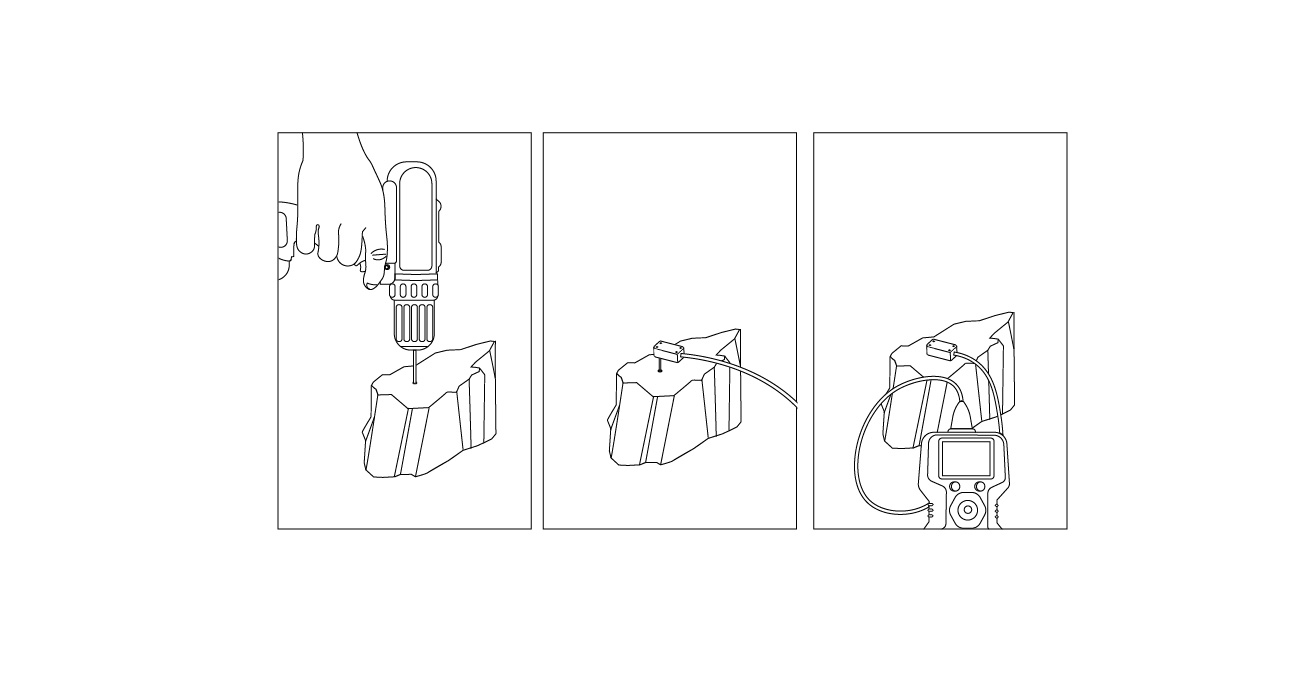
There are a few ways to measure thermal properties, but Fig. 8 walks us through the steps required to obtain thermal conductivity measurements from rock with the TEMPOS. The first panel on the left shows a hole being drilled very close in diameter to the needle of the RK-3 probe. Too big a hole will cause gapping, resulting in inaccurate measurements. The second panel shows the sensor correctly installed into the rock. The third panel shows the readings obtained on the TEMPOS handheld device.

Overall, the process of measuring thermal conductivity is fairly easy, as shown above. However, a few considerations must be taken into account to ensure accurate readings. The rock being measured needs to have a diameter large enough to allow several centimeters on every side of the probe, including below it, so the heat pulse will be contained within the sample.

The soil thermal conductivity can be measured in the field. The TR-3 (ASTM compliant) or TR-4 (IEEE compliant) sensors are ideal for this measurement. Simply insert the probe into the soil and take the reading. Measurements can also be made by taking samples from the field into the laboratory. Soil samples brought back to the lab usually require repacking to the density in the design. The thermal dryout functions are then determined in the laboratory.

Example of calculating thermal properties of a soil-rock mix

The best way to fully understand how to apply this model to real-world problems is to work through an example problem. For the purposes of this example, let’s assume a soil mix that is 60% by weight. We will consider anything less than 2mm in diameter to be soil and anything greater to be rock. The engineering specifications call for a final density of 1.8 Mg/m³, intending to be used as fill to cover buried cables. The stones within the mix are granite with a density of 2.65 Mg/m³ and a conductivity of 3 W/mK. The soil is moist and has a thermal conductivity of 0.5 W/mK. Lastly, we will assume that the stones are elongated, so we will use a shape factor of g_a = – 0.1.

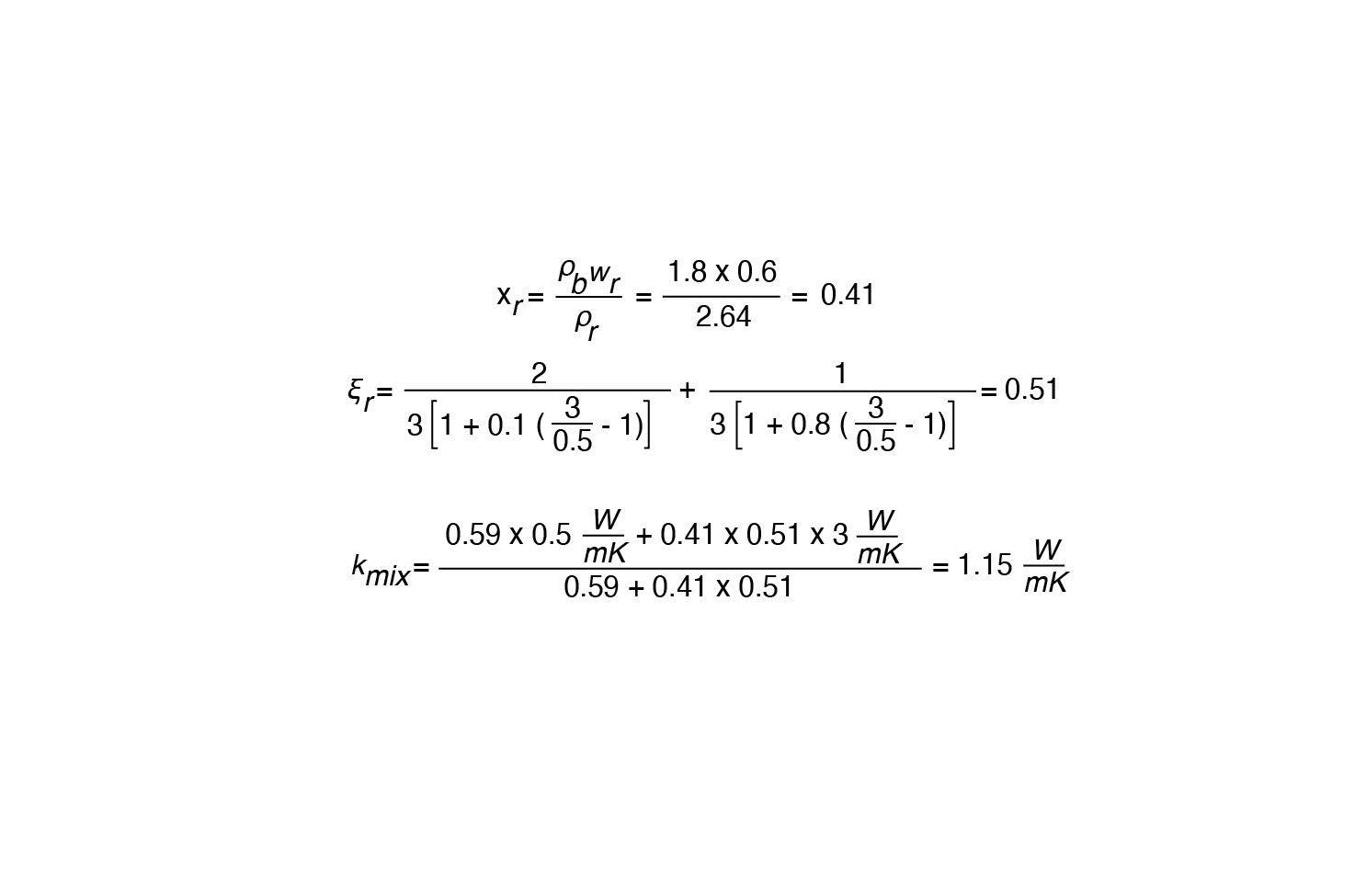
Fig. 9 works through the calculations one step at a time. The volume fraction of rock is calculated a little differently than we described earlier because in this case we know the final density. This computation shows that the rock, which was 60% of the total mix by weight, makes up 41% of the volume because the rocks are so dense. Computing the weighting factor results in the value of 0.51. Lastly, we compute the thermal conductivity of the soil and rock mix, resulting in a value of 1.5 W/mK.

Now that we have a value for the thermal conductivity of our mixture, it is important to check the value to see if it is indeed a reasonable number. There isn’t any way to make a direct measurement to ensure we have the right value without an enormous budget and a lot of work, but there are a few calculations that can be made to see if this number is reasonable.

We have determined that the rock has a conductivity of 3 W/mK and the soil has a conductivity of 0.5 W/mK. If we assume that those two are in parallel, we can use this calculation to check our work:

If we assume that the soil and rock are in series, this is the calculation we would compute:

We can expect the parallel calculation to be higher than our value and the series calculation to be lower. If your value falls between those two numbers, you can conclude the value you’ve found is reasonable.

Benefits of rocky soils

Some may view rocky soil profiles as the bane of their existence, threatening damage to expensive equipment or derailing progress. For others, rocky soil can be beneficial. In the case of buried power cables, the cables heat up underground, driving water away from the cable, and drying out the surrounding soil. This decreases the thermal conductivity of the soil, causing the cable to retain more heat, and creating the potential for disastrous damage. Rockier soils have a higher thermal conductivity, allowing the excess heat to be drawn away from the cable, preventing overheating. To learn more about this heat exchange and its impact on power projects read the following articles:

• Why Underground Power Cable Installations Need Soil Thermal Resistivity Measurements
• Thermal Resistivity: Real RHO Values for the Professional Power Engineer

Conclusions

It isn’t possible to directly measure the thermal conductivity of stony soil unless you have a sizable budget and a willingness for extensive labor. Probes can only measure the thermal conductivity of homogeneous media, leaving modeling as the only practical way forward . Luckily, with measurement of the thermal properties of the constituents with tools such as the TEMPOS system and determination of volume fractions, you can calculate a composite thermal conductivity that is at the very least as reliable as any direct measurement you might have made with exorbitantly priced equipment, with a lot less work and expense.

Questions?

Our scientists have decades of experience helping researchers and growers measure the soil-plant-atmosphere continuum.  

• Talk to an expert  
• Request a quote 
• Read the Researcher’s Complete Guide to Soil Moisture 

Watch the webinar

If you prefer to see a video, watch the following webinar where Dr. Gaylon Campbell does a virtual presentation of how to combine the conductivity of rock and soil to get the right value for the soil profile.