CONTRIBUTORS

Why K_fs is a pain

Saturated hydraulic conductivity, or the ability of soil to absorb water, has traditionally been a complex measurement for scientists to make.  Inaccurate field saturated hydraulic conductivity (K_fs) measurements are common due to errors in soil-specific alpha estimation and inadequate three-dimensional flow buffering.  Three-dimensional flow means water infiltrates the soil in three dimensions; it spreads laterally, as well as downward. The problem is, the value which represents saturated hydraulic conductivity, K_fs, is a one-dimensional value. Researchers use K_fs in modeling as the basis of their decision making, but to get that value, they must first remove the effects of three-dimensional flow.

Estimation—a risky proposition

The traditional method for removing the effects of three-dimensional flow is to look at a table of alpha values or the soil macroscopic capillary length. But since alpha is only an estimate of the sorptivity effect, or how much the soil is going to pull the water laterally, the risk of inaccuracy is high. And if a researcher or engineer chooses the wrong alpha value, their estimate could be significantly off.

To get around this problem, researchers sometimes measure K_fs with a double-ring infiltrometer (Figure 2), a simple method where the outer ring is intended to limit the lateral spread of water after infiltration and buffer three-dimensional flow. However, a double-ring infiltrometer does not buffer three-dimensional flow perfectly (Swartzendruber D. and T.C. Olson 1961a). So if researchers operate on the assumption that they’re getting one-dimensional flow in the center ring, they may overestimate their field saturated conductivity values. This can be disastrous, particularly when working with a soil that has been engineered to have a very low permeability. If K_fs is overestimated, a researcher or engineer could incorrectly assume a landfill cover (for example) is ineffective (K_s is over 10^-5 cm s^-1), when in reality, they’ve overestimated K_fs, and the cover is actually compliant.

K_fs—solved

The SATURO eliminates the estimation/assumption problem by automating the well-established dual head method. It ponds water on top of the soil and uses air pressure to create two different pressure heads. Measuring infiltration at these two different pressure heads avoids the need for estimating the alpha factor, enabling researchers to determine field saturated hydraulic conductivity without making any assumptions. Additionally, the SATURO uses much less water because it doesn’t require a large outer ring like a double ring infiltrometer. This automated approach saves time and reduces error in the hydraulic conductivity assessment. The following theory section explains in detail why this is possible.

See how SATURO readings compare with double-ring infiltrometer readings

In the video below, Dr. Gaylon S. Campbell teaches the basics of hydrology and the science behind the SATURO automated dual head infiltrometer. In this 30-minute webinar learn:

• What is hydraulic conductivity?
• Porous mediums
• What determines hydraulic conductivity
• Why you should care about hydraulic conductivity
• How is hydraulic conductivity measured?
• Lab instruments
• Field instruments
• The method behind SATURO: dual head infiltrometer
• Comparison: Double-ring and SATURO dual head methods

SATURO: Why it’s more accurate

Field saturated hydraulic conductivity, K_fs (cm/s) is a fundamental soil hydraulic property that describes the ease with which a fluid (usually water) can move through pore spaces or fractures under field saturated conditions. One of the oldest and simplest methods for in situ determination of K_fs has involved the measurement of ponded infiltration (D) from within a single ring (with a radius b) pushed a small distance into the soil (d) (Figure 1). The original analysis used the measured steady flow rate, Qs (cm3/s) and assumed one-dimensional, vertical flow to obtain K_fs from Bouwer (1986) and Daniel (1989).

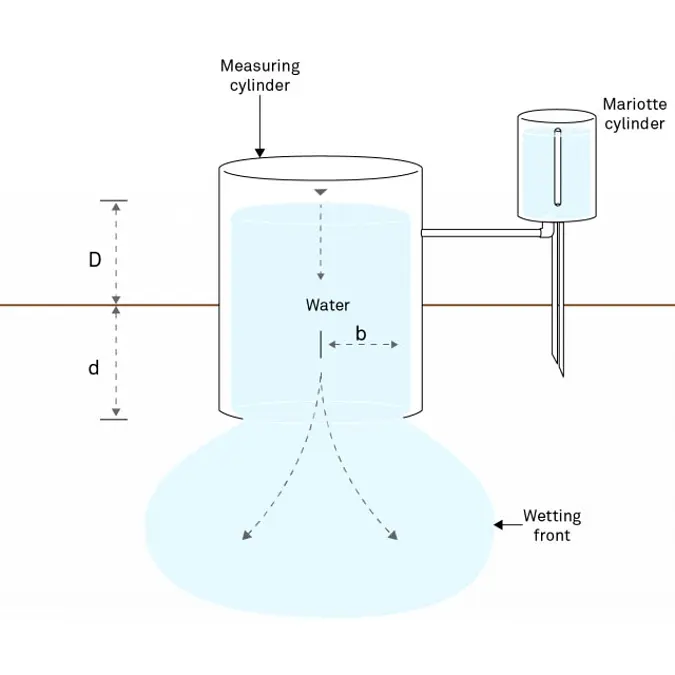
This approach overestimated K_fs due to lateral divergence of flow resulting from the capillarity of the unsaturated soil and from the ponding in the ring (Bouwer 1986). Attempts to eliminate flow divergence involved the addition of an outer ring to buffer the flow in the inner ring (Figure 2). However, the double-ring infiltrometer technique was ineffective at preventing lateral flow from the inner ring (Swartzendruber and Olson 1961a, 1961b).

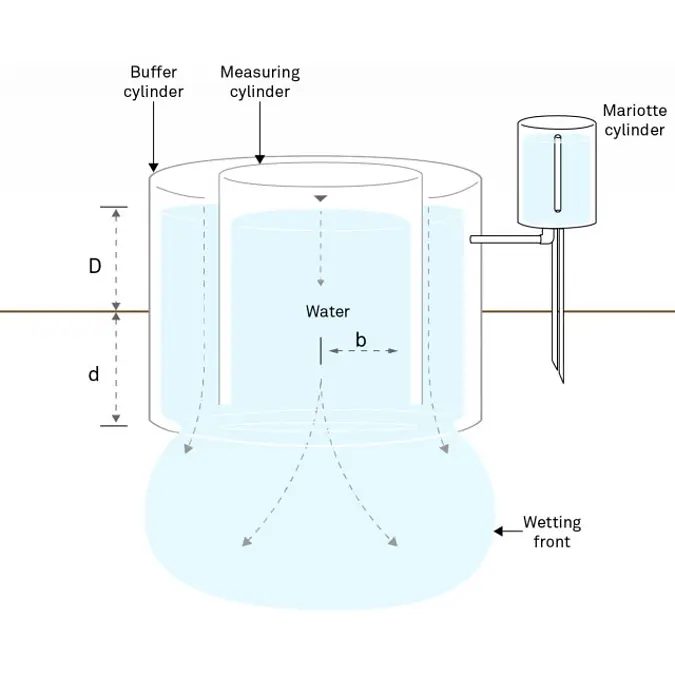
More recent research provides new methods for correcting for lateral flow. Reynolds and Elrick (1990) presented a new analysis method of steady ponded infiltration into a single ring, which accounts for soil capillarity, depth of ponding, ring radius (b), and depth of ring insertion (d) and provides a means for calculating K_fs, matric flux (φm), and macroscopic capillary length (∝). This analysis is known as the two-ponding head approach (Reynolds and Elrick 1990).

The two-ponding head approach is the technique used by SATURO, though with some modifications and simplifications. The simplest equation for this calculation is from Nimmo et al. (2009). They compute K_fs as shown in Equation 1.

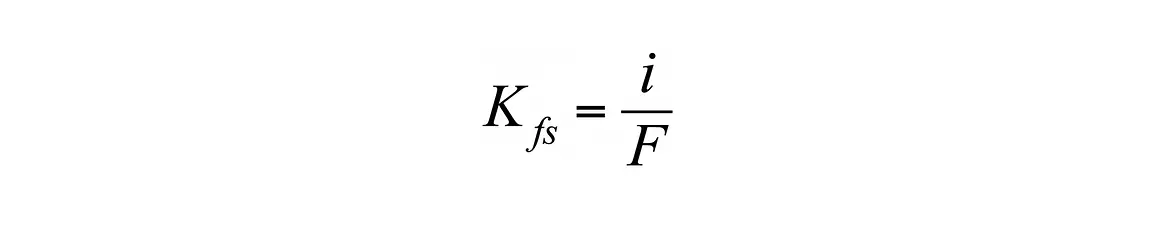
where i (cm/s) is the steady (final) infiltration rate (volume divided by area) and F is a function that corrects for sorptivity and geometrical effects.

Nimmo et al. (2009) gives F as shown in Equation 2

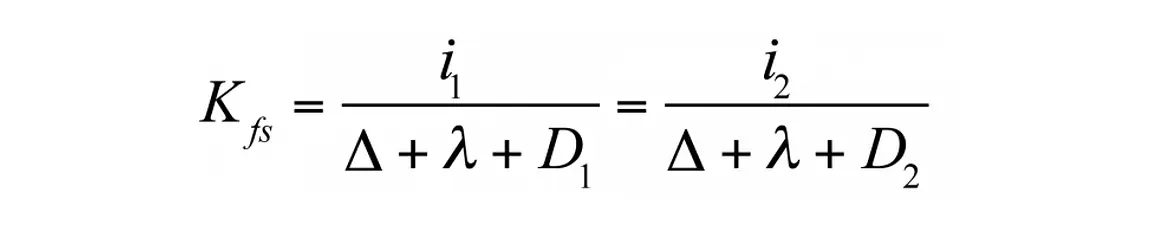
where

• D is the ponding depth (cm)
• d is the insertion depth of the infiltrometer (cm)
• b is the radius of the infiltrometer (cm)
• ∆ is the constant for a given infiltrometer geometry; C₁d + C₂b (cm)
• C₁ is 0.993
• C₂ is 0.578
• λ is the reciprocal of the Gardner ∝, which is a characteristic of the soil and its initial water content (cm)

In Equation 2, ∆ is simply Equation 36 of Reynolds and Elrick (1990) multiplied by bπ, which allows Figure 2 and Equation 2 to be reconciled with Equation 37 of Reynolds and Elrick (1990).

For two ponding depths, use Equation 3:

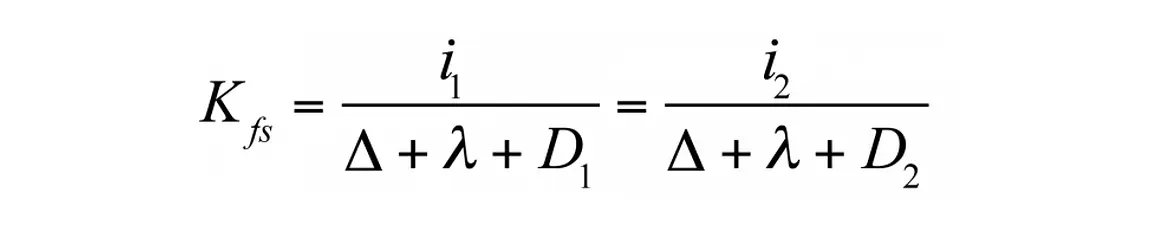
Rearranging one of the right terms to solve for λ in terms of K_fs, substituting this for λ in the other right term, and simplifying yields

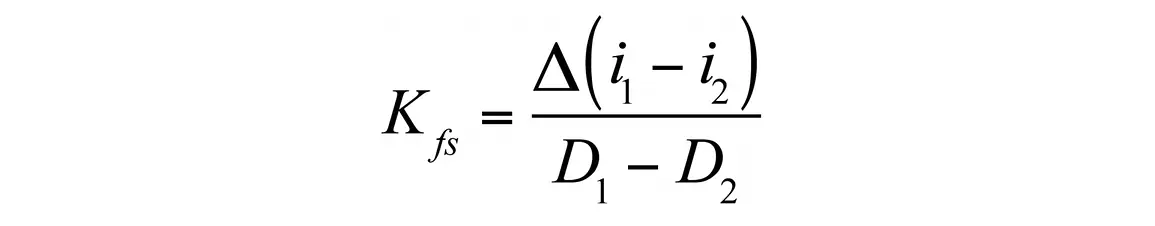
where

• D₁ is the actual high pressure head
• D₂ is the actual low pressure head
• ∆ is 0.993d + 0.578b (cm)
• i₁ is infiltration rate at the high pressure head
• i₂ is infiltration rate at the low pressure head

For ∆, d is the infiltrometer insertion depth and b is the infiltrometer radius. For the SATURO, 5-cm insertion ring, d = 5 cm and b = 7.5 cm, so ∆ = 9.3 cm. For the 10-cm insertion ring, d = 10 cm and b = 7.5 cm, so ∆ = 14.3 cm.

The hydraulic conductivity is then multiplied by the difference in quasi-steady state infiltration rate for the last pressure cycle and divided by the difference in the measured pressure head from the last pressure cycle.

Equation 4 is equivalent to Equation 41 from Reynolds and Elrick (1990) and removes the dependence on soil characteristics and initial water content described by λ.

Save hours of tedious manual labor

The SATURO combines automation and simplified data analysis together in one system. It even computes infiltration rates and field saturated hydraulic conductivity on the fly. The SATURO makes life a little easier for those who need a faster, more accurate way to measure K_fs in the field.

Questions?

Our scientists have decades of experience helping researchers and growers measure the soil-plant-atmosphere continuum.

• Talk to an expert
• Request a quote

References

1. Bouwer H. 1986. Intake rate: Cylinder infiltrometer. In Klute A., editor, Methods of soil analysis: Part 1—Physical and Mineralogical Methods. 2nd ed. Madison (WI): ASA and SSSA. 825−844. (Article link)
2. Dane JH and Topp GC, editors. 2002. Methods of soil analysis: Part 4—Physical Methods. Madison (WI): Soil Science Society of America Inc. (link)
3. Daniel DE. 1989. In situ hydraulic conductivity tests for compacted clay. J. Geotech. Eng. 115(9). (Article link)
4. Nimmo JR, Schmidt KM, Perkins KS, and Stock JD. 2009. Rapid measurement of field saturated hydraulic conductivity for areal characterization. Vadose Zone J. 8(1): 142−149. (Article link)
5. Reynolds WD and Elrick DE. 1990. Ponded infiltration from a single ring: I. Analysis of steady flow. Soil Sci. Soc. Am. J. 54(5): 1233−1241. (Article link)
6. Swartzendruber D and Olson TC. 1961. Sand-model study of buffer effects in the double-ring infiltrometer. Soil Sci. Soc. Am. Proc. 25(1): 5−8. (Article link)
7. Swartzendruber D and Olson TC. 1961. Model study of the double ring infiltrometer as affected by depth of wetting and particle size. Soil Sci. 92(4): 219−225. (Article link)

Take our soil moisture master class

Six short videos teach you everything you need to know about soil water content and soil water potential—and why you should measure them together. Plus, master the basics of soil hydraulic conductivity.

Watch it now