Dr. John Norman shows how to use a single-ring, dual-head, ponded infiltration technique with the analysis of Reynolds and Elrick to get key parameters for use in a macropore infiltration model. These same measurements can also be used to obtain values of the saturated hydraulic conductivity, which is useful for traditional infiltration models such as the Green and Ampt formulation.

Macropore models that include characterization of the geometry of the macropores tend to be complicated and require more parameters than can be determined from a reasonable set of independent measurements. The M&M model is a relatively simple macropore model that requires only nine parameters. Three or four of these can be determined from a standard description of soil structure. One comes from the Coefficient of Linear Extensibility and four or five are obtained from ponded-infiltration and hydraulic properties measurements. This webinar will focus on the ponded infiltration measurements. The parameters from hydraulic properties will be the subject of another seminar.

Next steps

• Read more: Accurate field saturated hydraulic conductivity—Why is it so difficult?
• Related webinar: Soil Hydraulic Properties—8 Ways you Can Unknowingly Compromise your Data
• Take a look at the SATURO infiltrometer
• Request a live ZENTRA Cloud demo

Questions?

Our scientists have decades of experience helping researchers and growers measure the soil-plant-atmosphere continuum.

• Talk to an expert
• Request a quote

Presenter

Dr. John Norman, faculty member of the Department of Soil Science and the Department of Atmospheric and Oceanic Science at the University of Wisconsin since 1988.

Transcript

LEO RIVERA 0:10
In the detailed plant environment model named Cupid, with applications to agriculture, ecology, forestry and meteorology. Current efforts focus on assisting farmers with management decisions that maintain yields and minimize environmental degradation through precision farming techniques.

LEO RIVERA 0:28
My name is Leo Rivera, a product manager with Decagon Devices. I will be your host and moderator for this webinar. I first need to go through a few legal items in regards to the seminar. Let me start by saying that this seminar is under copyright. However, these seminars are great educational tools, and we don’t want to discourage you from sharing them with others. But due to copyright, we ask that you contact us first in writing if you would like to use any of the information in the seminar or slides. We have formally allotted 60 minutes for today’s program. The seminar portion will last about 45 minutes with about 15 minutes at the end for your questions. You can send your questions to us throughout the event using the questions feature. We will get to as many of your questions as possible, and any unanswered questions will be addressed after the event. The webinar is being recorded and an archived version will be available for your review this time next week. In a week, we will send you a follow up email with instructions for accessing today’s event, as well as a link to download your certificate of participation. Unfortunately, the seminar will not be available before this time. Right after the webinar, a short survey will pop up on a separate webpage window. We use these surveys to determine what the content of our next webinars will include, among other things, so please take a few minutes to give us your feedback. I will now turn the presentation over to Dr. Norman.

JOHN NORMAN 2:01
Hello, everyone, this is John Norman.

LEO RIVERA 2:15
Sorry, folks, one quick second, we’re having a slight difficulty.

JOHN NORMAN 2:49
Well, this morning, I would like to visit with you about measurements to parameterize a macropore model. A bit of an outline here, introduction, I describe this model a little bit in order to give you some background concerning the parameters that we’re trying to get from the measurements. And then I’d like to spend a little more of the time on the actual infiltration measurements themselves. Estimating the characteristics of these macropores slit with head sizes as you’ll learn more about and some about the actual saturated hydraulic conductivity. So macroporosity is really a key part of soils. These huge pores that are all connected in the soil are really the lifeblood of the soil. And they have a profound influence on the water and solute movement in the soil. So you might ask, Well, then why do we usually neglect these macropores in our modeling of the soil. many of the models of the soil don’t really distinguish the macropores in particular. And we wonder Well, why is that the case? Well, because more often than not, rainfall rates actually control infiltration into the soil so that complications from macropores can be neglected. But sometimes, on rare occasions, you get huge rainfall events. And then dealing with the macropores explicitly becomes a critical part of understanding what’s happening to the moisture in the soil.

JOHN NORMAN 4:28
I’ll give you a couple of examples here. One of them is that if we look for tabulated saturated hydraulic conductivity estimates for silt loam soil, and these come from Rawl’s publications, there’s probably a dozen of them. It’s about seven millimeters an hour, but when we did some experiments on a plano silt loam in Wisconsin, we found that we had drainage rates at one meter depth of 750 millimeters per hour, so that’s 100 times bigger. But if you use the saturated conductivity estimates from Rawls over the season, it gave you a reasonable total drainage. So the rainfall rate controls so much of this that you can ignore them a lot of the time. Another example here, we had 114 millimeters of rain — that’s about four or five inches of rain — in half a day on a clay loam soil with a lot of clay, had a maximum intensity of three inches per hour and the measured runoff was almost zero, I mean a fraction of a millimeter. And the modelled runoff if you use the saturated conductivity 10 times as big as the tabulated one, was still 20 millimeters of runoff. But if you use the macropore model, there was no runoff because these cracks, as you can see in this picture here, absorb that moisture so effectively that there was no runoff. So your estimates of the soil storage during this period of time following this rain would really have quite large errors if you weren’t dealing with the macropores themselves.

JOHN NORMAN 6:08
So the idea here is to look at a simple macro pore model. Simple is a relative term, of course. There are macropore models in soil physics, many of them in fact, but most of them, at least that I’ve looked at, are either extraordinarily simple, not really using characteristics of the soil you’re working on but just sort of a coefficient for fast moving water, or they are so complicated, you can’t get all the parameters. So the idea here was to create a model that you could parameterize independently of what you were trying to predict, the water status of the soil. So, this model is simple, it deals with the soil structure and root channel effects. It uses a cubic geometry, which is of course, obviously very simple. It has constant interaggregate spacing as a function of depth so that the slits that the water is going down in the holes, the water is going down are a fixed size. And that is laminar flow in these slits, no pressure effects, no bottleneck. So this is really a pretty simple system. And the water moves from the slits into the bulk of the soil through Darcy flow. So you’re moving from these macropores next to the peds into the peds with a Darcy flow, and we include the shrink swell of the soil. And then ultimately as the infiltration is going on, we want to link these macropore equations into the Richards equations for redistribution after infiltration. So Richards equation, you may run on, say a 15 minute time step, in between the runs of the Richards equation, he would run the macropore model, and then it would change the moisture content, and you would update the Richards equation. So this model doesn’t run on its own. It runs in conjunction with the Richards equation, because after all, some water does move from ped to ped as well as moving down the macropores.

JOHN NORMAN 8:14
So if we think of this image here, on the left, you have this cubic sort of geometry. It’s not quite cubic, I mean, there is prisms deeper down there, but what we use in the model is cubic. And you can see this equation for the macropore flow, laminar flow in the slit. And as water moves down through these slits, there’s a couple of key parameters here. One is this Wped which is just ped width. And this ped width changes as a function of depth. But it also changes with water content because of the shrink swell characteristics. The other key parameter is something we’re going to call 2Bped. 2Bped is this slit width, right. And this is a key parameter. These two parameters you can see appear in this equation. And this, the slit width here, there’s 2Bped, you can see is cubed in this equation. So the slit width is a very important factor in determining how fast water moves through the system. And of course, there’s some other quantities in here: density, gravity, viscosity. And this theory is developed more completely in this publication by Brian Lepore in 2009 and geoderma. So you’ll see that reference show up here this morning. So we have a simple expression, relatively simple expression, for how fast water is likely to be moving through these slits. And once they get into the slit, of course, that water is going to move into the soil peds. And you can see this sort of cartoon here of how this water moves from the macropores into the peds. And the ped width is again important, because it affects how long it’s going to take the wet that ped up, but also the saturated conductivity of the ped itself. That’s a very key part. And then there’s some other quantities of porosity, gravity, the moisture release characteristics, the air entry potential, the power, and this expression. That comes from Gaylon Campbell’s work in 1974.

JOHN NORMAN 10:29
So there’s some moisture release hydraulic parameters that we need to characterize this ped as well as its saturated conductivity. So you can see there’s kind of two equations here, there’s one for the flow in the macropores, and then a second for the flow from the macropores into the peds. Again, a fairly simple approach to this. If we look at these parameters, we have nine parameters in this m&m model. And there’s structural parameters, which determine the size distribution of these peds as a function of depth. And then there’s hydraulic parameters that determine how the water moves. And we’d like to start out with the structural parameters. This W ped zero, which is that ped size at the surface, and then a W ped max, a ped size at a deeper depth. And then the distribution of these ped size and then a curve fitting sort of coefficient. So if we think of the structure in this plano silt loam, which we work with in Wisconsin, it typically has granular structure at the surface, and then a platy structure below that, and then a subangular blocky structure below that, and ultimately a prismatic structure deep down. And so if we think about the structure, and structure is really nothing more than a collection of the individual particles into larger assemblages of the larger chunks, we call aggregates or pits, what we do is we generally just fit this as a function of depth from the soil description. So the soil survey describes this structure, describes the size and the stability and all these different characteristics of the structure. So we fit a curve to this, and the structure generally gets larger and larger with depth. And the W ped zero is up here at the surface. And the W ped max is the size of the peds deep down. And C is a sort of ped size somewhere in between. And this h coefficient you see here controls the shape and steepness of this curve.

JOHN NORMAN 12:40
And you can see here in a table that’s taken from the soil survey that there’s sizes. Generally the soil pedologist and the classification people, use words — very fine, coarse, thick — but they have a dimension associated with all of those. So we can use those dimensions that we have here for platy or prismatic or whatever, we can use those dimensions, then as a basis for establishing the structural characteristics of this soil as a function of depth. In this equation you see in the upper right hand corner here, is the mathematical form of that equation. Again, you see the W ped zero, W ped max here, the h, C, and the h controls the shape of this curve. If H is one, the shape is kind of like the curve you see here, if it’s two, that becomes more of a sigmoid, so you have a lot of flexibility to fit how the structure changes as a function of depth. So you’re really trying to get this W ped as a function of moisture content and depth. So it’s a structure based function of depth, and this water content causes it to change a little because of the coefficient of linear extensibility or the shrink swell on the soil.

JOHN NORMAN 14:01
So we get these initial values for this equation from the structural descriptions, from the soil survey or from a description of the soil. And we might want to refine this W ped max term with the saturated conductivity depending on what approach that we might use. So, as you get deeper, all of the cleavage planes may not be conducting water. and the effective size at the deeper depths might be different than the ped size you get from your soil description. So that’s the structure parameters and we have a series of hydraulic parameters here. This coefficient of linear extensibility that you see, the air entry potential, the power, and the moisture release equation, saturated conductivity of the ped, then the slit width for these macropores and the size of the macropore, of the structural element of the ped itself at the deeper depths. So we really have this set of hydraulic parameters. And I want to concentrate more on those this morning.

JOHN NORMAN 15:06
This coefficient of linear extensibility. I don’t know how familiar you might be with that, but it’s recorded in the soil survey. So often this is a number you can just look up for the particular soil that you’re working. And you can get a coefficient of linear extensibility and then there’s a correlation between that and the real one. And it can be done quite quickly, if you don’t happen to have the tabulated value. So this is a standard coefficient that soils people have been measuring for decades. Now, these hydraulic parameters that control the moisture release curve here and the saturated conductivity, you can measure with standard methods and Decagon provides some equipment that you can use to measure these quantities, your moisture release curve, the water content at different potentials, and then from that estimate these parameters. And so there are standard methods to do this. But there’s also lookup tables that you can use, like this table 9.1 from Gaylon Campbell’s book in 1998, which is taken from the work of Rawls, one of his sets of data that he released. And you can see here, you can get the parameters that you need from just the texture itself. So these coefficients can be obtained fairly easily and independently. It’s pretty straightforward, but the ped hydraulic conductivity is not the same as the soil hydraulic conductivity. There’s a difference between the two because peds are coated with organic matter that plugs pores, and they’re coated with clays and such, and so their conductivity is systematically smaller. And one of the papers that made some measurements of this found a factor of 3.5 between the ped when it was coated and the ped when it was not coated. And so this is a coefficient in the macropore model that probably needs a little bit more work to understand a little bit better. But you don’t use that conductivity from the soil estimates from tables directly. It’s smaller for the ped.

JOHN NORMAN 17:54
We have had several methods for determining the slit width. This is a really challenging quantity to determine. And it’s cubed in the equation. So you have to do it with some care. The first method is to calculate the saturated conductivity of the soil or calculate the Bped from a measurement of the saturated conductivity of the soil. And then you equate that saturated conductivity to the macropore flow at a deeper depth. And if we look at that, revisit that macropore equation, you can see it looks a little complicated to solve for 2Bped. But if you assume that the Bped is much less than the Wped, that is that slip with is a lot narrower than the ped size, and typically it’s 100 to 1000 times smaller than the ped size, is you can neglect that in the denominator here, this 2B where it’s added to the Wped. And then this becomes a very simple equation and we can just solve it for 2Bped by equating the saturated conductivity to the macropore flow and you get a simple equation for the slit width at a deep depth. So this depth we’re working with here is the wetted depth of the infiltration. It might be a half a meter deep or even deeper, typically at the depth of the maximum pore size. And so this is a approximation, but this is one way in which we get this macropore slit width. It’s fairly straightforward, but then we need a good measurement of the saturated conductivity to do this.

JOHN NORMAN 19:32
A second method would be to take cores from the upper portions of the soil, typically the top eight or 10 inches of the soil, and we use a three inch bulk density sampler or a 7.6 centimeter bulk density sampler. You take these cores, extract them, and they’re in a little aluminum ring, and you saturate that sample, right. So you have this sample that’s relatively undisturbed inside of this aluminum ring, three inches in diameter, three inches long. And you saturate that sample, and then you weigh it. And then you put the rings on a porous plate hanging column of water about 25 centimeters long, and allow that suction to drain just the macropores, then you weigh it again, and you can get the fraction of macropore volume. And when you combine that with the ped size in that core depth you work with, you can solve for a slit width or a Bped, a 2Bped factor. And it’s pretty straightforward. And then you assume that this is appropriate all the way down for all of the depths in the soil, right. And if we do that, we would like to revise the Wped max because it might be larger than the actual structural ped size in the soil, right. So we refine that at a steeper depth by using the same procedure in the same macropore equation that we used to solve for the Bped. But this time, we’re equating this saturated conductivity to the macropore flow, but we’re using the Bped that we determined from the core samples at the surface. And if we solve that same equation, we can solve for this ped, this maximum ped size, recognizing that the saturated conductivity is an appropriate estimate of the macro pore flow at the deeper depths.

JOHN NORMAN 21:35
So there’s two methods here for estimating these two critical parameters, the size of the peds as a function of depth, and the slit width. And these procedures that we just described can be, we can obtain the parameters from these with ponded infiltration measurements. That’s really what I want to emphasize here now, is these ponded infiltration measurements. As a sidelight, we — just as a side comment here — undoubtedly, if the soil is saturated and the macropores are empty, the shape of this ped size versus depth curve undoubtedly contains information about the — is related to the infiltration curve as a function of time. So if we look at the shape of the infiltration curve, it’s really reflecting how the macropore network is changing as a function of depth. And as we go deeper, there are fewer macropores, and the conductivity or the infiltration rate goes down. So we could actually do experiments on this, I mean, we could make a measurement of the saturated conductivity and just by a normal method takes an hour or two, then we could wait 30 minutes for the macropores to drain, but that’s not long enough for the peds to dry out. We could then reinfiltrate that thing and get a pretty careful measure of the vertical distribution of the macropore network. But we haven’t done this. So this is something that is yet to be done. And it’s an idea that would be fun to explore someday, or maybe some of you out there would explore this.

JOHN NORMAN 23:37
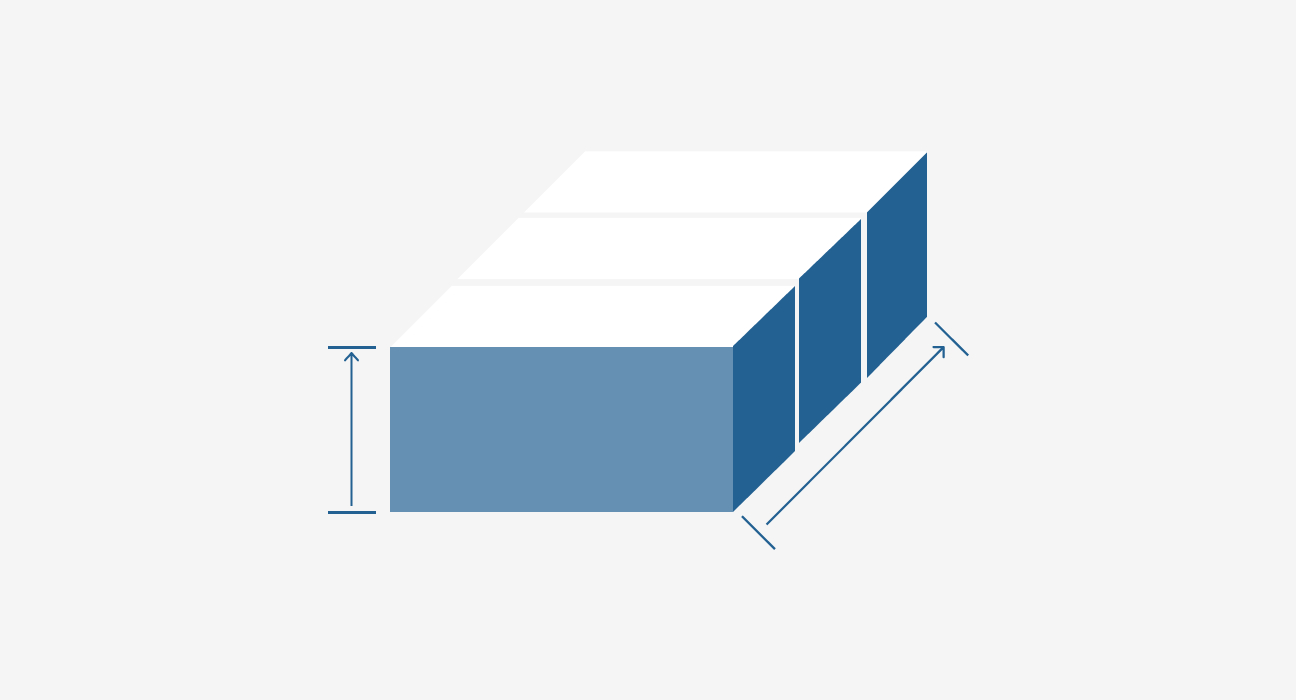
So we want to get to these ponded infiltration measurements, I mean, because those measurements are going to be the key to getting at some of these macropore quantities, particularly the slit width and the ped size as a function of depth. So we’re going to use a method of Reynolds and Elrick. This is a method that I’ve used a lot. And I’ve really begun to appreciate a great deal how powerful this method is. It’s 20 years old now. But it works just as well now as it did 20 years ago. It says single ring dual head measurements, lots of people like dual ring, double ring infiltration measurements, but when you have macropores in the soil, double ring doesn’t really work quite the way you’d like it to. And so this single ring is easier, uses less water, and has some real advantages. So these measurements are pretty straightforward and they can be done in maybe one to at most two hours, typically a little over an hour, an hour to hour and a half is all it takes to do these measurements on the site.

JOHN NORMAN 24:54
So what equipment do we need? Well, we need a ring that’s going to hold the water. And so we use a heavy gauge sharpened stainless steel sharpened on the bottom so you can pound it into the soil. And it’s tall, because we’re going to use two different head levels. So this ring has to be tall enough to handle both heads. We’re going to use some bentonite that’s going to seal that ring around the edge and a squirt bottle with some water to wet that bentonite so that we don’t get any leakage down the edge of the ring. And then we’re going to have a little reference, a disk with some reference points on it that have the two heads that we’re going to be making measurements with and some legs where you can push it into the soil so it stays fixed. We need some graduated cylinders in order to measure water, the rate at which water is infiltrating, and we modify them a little, as you can see, with stoppers and the ring stand to hold them. And of course, we need car boys to haul the water around and to fill up with this .01 molar gypsum so that we don’t disperse the soil surface. And a stopwatch. So it’s all pretty garden variety equipment, nothing fancy here. It could be improved quite a bit if you use a little more elegance in these measurements. And maybe someday, Decagon will make something that will make this measurement even easier than it is now.

JOHN NORMAN 26:22
Well, you might guess that with a single ring, you’re gonna have divergence and Reynolds and Elrick thought about that, and they correct for it. It does make homogeneity assumptions like we do with a double ring. But it does correct for this divergence that’s going to happen below this ring when you insert it. But we standardize these conditions, 25 centimeter diameter ring, 10 inches, five centimeters into the soil or 2 inches. And so we can use the results from Reynolds and Elrick to correct for this, and it seems to work pretty well. And we made a special insertion tool so we can pound these rings in and do dozens and dozens and dozens of these measurements with the same rings without banging them all up. And we have to be careful that we seal these rings around the edge with bentonite. You don’t have to do much of that if you use this insertion tool, because the rings go very straight into the soil. They don’t wiggle and cause cracks and gaps next to it. So this is a look at one of these rings. It’s about 10 inches tall. There’s a little black ring around the bottom here for the two inch insertion depth. You can see the pounder here and this special insertion tool. Here they’re put together with the level on there, so you can pound it straight into the soil. And you can see what the bottom looks like. So this thing helps us to install these quickly, efficiently, easily, and with great reliability. And then of course, we have to seal them with the bentonite. And you can see here this disk that we’re going to dribble the water in so it doesn’t disturb the soil surface with this two reference points here on it that we’re going to control the water level with. So we use this .01 molar gypsum and the water so we don’t disperse the soil and plug the macropores. We use two ponding depths of two inches and seven inches.

JOHN NORMAN 28:22
And we can get very accurate height control with these sharp pointed rods, right. And we do that by raising the water level a little bit above these points and then letting it fall. And as it falls, when that point just distorts the surface of the water, when the surface tension just gets bent a little bit, you can see that really easily. And that’s when you make your time estimates. And so you’re always making the estimates when that water level is dropping slowly, and it just hits the point of that reference rod that’s sticking up in there. And you can measure these levels to a fraction of a millimeter. It’s just remarkable how straightforward that is to do. But this plate should be a little off of the soil. So it’s typically up about a centimeter. So these rods are actually four centimeters long and 16.8 centimeters long in order to let the water infiltrate underneath this plate. We typically fill up this two liter graduated cylinder. We start with two liters because you don’t know how fast the water is going to go into the soil where you happen to be. And then we have another beaker that has a couple of liters of two or three liters of water in it. And we pour that into the ring first in order to fill it up above the level of that reference point for the two inch head, let’s say, that we’re going to start with. And you pour it onto this aluminum plate so you minimally disturb the soil.

JOHN NORMAN 29:54
And then you can start making your measurements. So you fill up your cylinders here with the water. Put the stoppers in the end with their little tube sticking out of them. And then you fill this thing up with water, and just above this point right here, you can see that reference point is just barely breaking the surface. And you can measure this level very accurately, if you’re always going down, when you do that time measurement. You have the stopwatch here, the beaker you fill it up with, and the graduated cylinder here, you’re gonna put this tip underneath the water. So you put your finger over the end, put the tip underneath the water, and no water will leave that graduated cylinder until you lift it up above the water level. So you can control the addition that way and keep the water level just above this fiducial point, this reference point, until you want to make the measurement and then you let it go down and let the point just break that surface. And when the cylinder has dropped down with that tube below the water level, no water comes out of the cylinder. And so it’s a pretty simple method for doing it. Here, you can see the water level as well below the tip of that of that particular reference point. Right.

JOHN NORMAN 31:12
And so it’s a method you can use in the field that doesn’t require any power. You’re pretty busy while you’re doing this, because you have to record all of this data as well as monitor these reference points. I mean, here you can see some of the equipment, the pounder and water supply and such. So now, you take the measurements the first minute — after the first minute, and then every two minutes. And it’s good to start this process fairly quickly. Then after 20 minutes or so, you add about six or seven liters of water to this ring to get it up above the seven inch. And then you go through every two minutes and you’re making measurements with the seven inch head. And then you either dip that water out or siphon it out, get back down to two inches, do another 20 minute set of data at two inches. And then you pour the six, seven liters back in there and do another measurement at seven inches. So you can see you’re doing a series of measurements here at the two heads. And the data when you’re done looks something like this, where first you have the first infiltration that you’re doing, starts appear, these are infiltration rates on the y axis to millimeters per hour. So you see we’re starting well over 1000 millimeters an hour. This is a meter an hour infiltration rate. So this soil can conduct a lot of water under these conditions. And you go for 20 minutes here, and then you put the seven inch head in, which takes you a few minutes to get in there. And then you have 20 minutes of the seven inch head and then drop back down and you do another 20 minutes with the two inch head and then another 20 minutes of the seven inch head. So now you’ve got the data that you need to fit two curves to this in order to obtain this equilibrium value out here, this infiltration rate after a long time. And you can see here we’ve gone about 4500 seconds, which is hour and 20 minutes or so, which is pretty typical for these experiments. And we’re not going to carry it all the way out to a long time like 2, 3, 4 hours. We don’t need to because we can see where these curves are going.

JOHN NORMAN 33:33
So we fit those curves in with a very simple exponential a plus b times e to the minus c times time. And these coefficients a plus b represent the initial infiltration rate, that is where that exponential curve intersects that Y axis. And the a value itself is the long term infiltration rate that we would expect to have if we did this experiment very long — over a very long time. We don’t really want to do this experiment over a really long time because the water gets so deep in the profile that it’s being influenced strongly by conditions at a depth that we really aren’t too interested in and we know these soils are not uniform. In fact, many of these soils are silt loams over clays or silt loams over sand. And so we can’t really let this go that long in order to get this data, otherwise the water is in the sand and measurement we get isn’t reliable. Right.

JOHN NORMAN 34:39
So this a then is this asymptote or this cue, this flux, this infiltration rate after a long time — this sort of asymptote that this exponential is going to. And we can use the equation from Reynolds and Elrick. The saturated conductivity is a shape factor divided by the radius of the ring, times the difference in the flow rates at the two heads, divided by the difference in the heads themselves. Now, this shape factor, Reynolds and Elrick spent a lot of time trying to figure out how to do this shape factor. And they’ve done it fairly meticulously. And we’ve just looked up the value from their paper, and we use the 0.31 for the particular ring configuration that we’ve chosen, which is a 10 inch ring, pushed two inches into the soil. And so here’s data from that graph that you saw here, this graph, so we take this graph, we fit those curves to it. And this is the result of that. We had 340 millimeters per hour at the seven inch head, and we have 230 millimeters per hour at the two inch head. We convert the units on those. And these are the units in centimeters, 17.8 centimeters for the seven inch head, five centimeters for the two inch head, and we get a saturated conductivity of 106 millimeters per hour. So you might say, Well, why is the saturated conductivity so much lower than the asymptote is for the two inch head? And well, part of the reason is, is that there’s two inches of head on there, and the saturated conductivity corrects for that. But the other reason is that there’s divergence from the single ring, and that correction is being done on that divergence to estimate the saturated conductivity. So it’s quite a bit lower than that long term infiltration rate.

JOHN NORMAN 36:39
Well, if we have this saturated conductivity that we’ve estimated, we can get the macropore slit width that we talked about before by method one. In that case, this is the equation, just back the one we referred to before, that the bped is 1/3 power of the saturated conductivity times the viscosity times the head size divided by the density times gravity. So we can use that equation. On the left side here are all of the parameters that we put into this equation. The viscosity here is a viscosity at 20 degrees. It does depend on temperature, and so you can adjust that some based on your temperatures. But, if we do that, the 2bped we get is 166 microns or 0.166 millimeters. So this is the estimate that would come for the slit widths by method one. And in the process of doing that, of course, we’ve gotten our Wped zero. And our Wped max, that is the structural ped size to the surface and the structural ped size at deeper depths from the structural description of the soil itself. So we excavated the soil, and we characterize those ped sizes for our particular site.

JOHN NORMAN 38:10
We can also do method two. We can use this bulk density sampler, we can take cores at several different depths and use this equation that relates ped size macropore fraction to the ped width wherever we took the cores. In this case, we took cores at two depths, between two and a half and 10 centimeters, which we called six centimeters, and between 15 and 22 and a half centimeters, which we called 18 centimeter depths. We took eight cores at each depth and got the mean and standard deviation for the macropore fraction. And that’s .0175 for the shallow core and .008, that’s 1.75% macropore space in the shallow core and .8% natural pore space in the deeper core. And from that you can calculate, then, the spacing which comes out at 175 microns for the shallow core and 160 microns for the slightly deeper core. So this is encouraging because the second method gives us a result that’s pretty close to the first one. We can then use this equation for macropore flow rates and solve for the ped size at this deeper depth. That deeper depth is somewhere around half a meter or so in this case, and using that saturated conductivity to get that maximum ped width that comes out to the .2 meters, which was the same .2 meters we assumed here. So all of these are consistent enough to give a set of values that close on themselves. So it’s pretty fascinating process.

JOHN NORMAN 40:31
So how have we used this? What did we do with this? I mean, we got a method here, and we’ve experimented with it. But we had a 10 acre field that we worked on. This is a farmer’s field. It’s 10 acres, its slope varies from zero to about 25%, depending on where you are. And the texture across this field varies. This upper left hand corner here you see a map of the clay percentage as a function of space over this field. And then in the middle here, you see a map of the sand distribution with space on this whole field. And you can see the clay varies from about 15% to maybe 40%. And the sand varies from, you know, maybe 5% to 50%. So there’s a lot of variation. And based on this texture map alone, we can use the standard curves for saturated hydraulic conductivity to produce the hydraulic conductivity map you see in this lower right hand corner.

JOHN NORMAN 41:38
So this is all modeled at this point. You say, Well, is this worth anything? I mean, how well does this work? Can you model it like this from this detailed map of texture? These little grid squares you see on here, each one of those is five meters. So each little square you see on this thing here is five meters by five meters. This map was created by a company called Earth IT in Madison. And they do this mapping now as a matter of course, for their company. So we then went into that field. Here the color is elevation. So the red is the top of the hill, the blue is the bottom of the hill. And you can see here with this 3D map from MATLAB, you can see the elevations better. But here, it’s sort of flat and the color covers the elevation. And then these dots, every one of these dots is where we made these infiltration measurements. And if the dot is a light color, like this white one right here, that’s a very high infiltration rate, maybe a saturated conductivity of 500 millimeters an hour. And the middle gray are medium infiltration rates and the black ones are the low infiltration rates. So if we map this or draw a frequency distribution of this over this field, what does it look like? Well, those measurements look like this heavy line here. These are the measured values, graphed out like a log normal distribution. This is 20 or 25 measurements that were made in this field over a few days. These other dotted lines you see are various assumptions you would make about various depth intervals of texture in order to map this. And so that texture map doesn’t produce that unreasonable distribution of hydraulic conductivity. So the way we want to model this field is that we want to have a distribution of saturated conductivities over this field when we run it in this precision agricultural landscape modeling system. That’s what this PALMS stands for here. It’s a three dimensional model of plant processes meant for agriculture.

JOHN NORMAN 43:52
So, we have a pretty practical method here that works remarkably well. And with these measurements, these infiltration measurements, you can compute some other quantities, if you make some homogeneity assumptions, that are useful in soil physics, that matrix flux potential, or the sorptivity, or the macroscopic capillary length, or the characteristic mean pore radius, or wetting front potential. So these measurements are remarkably powerful. And this method that Elrick has created is a very, very useful method. And with the two heads, you can make these estimates of saturated conductivity with minimal assumptions. So we have something here, I think, that provides us with a very powerful tool for characterizing fields and the distribution of water character, of hydraulic properties across farm fields. So with that, I’d be happy to entertain questions that people might have.

LEO RIVERA 45:00
All right. Thank you, Dr. Norman. As I stated at the beginning of the presentation, you can send your questions for Dr. Norman through the questions feature. Our first question is: John, can you comment on the application of the approach in a situation like vertisols, with swelling clays where the size of the cracks may change over time?

JOHN NORMAN 45:29
That’s a fascinating example. When we did this work originally, we had in mind these vertisols in Texas, because the graduate student who really pioneered this whole macropore approach was Christine Morgan, who’s a faculty member at Texas A&M. And a good portion of what I presented here to you today on this macropore model was her PhD work. So we had this in mind, which was why the coefficient of linear extensibility is an integral part of this. And we do believe that this approach is relevant to the vertisols, to the shrink swell clays where you have these huge cracks. Now, there is a difference, and we assume something different about the geometry here than you actually see. And so you might have some reason to doubt the relevance. And that is that we widened the crack between each ped. I mean, that’s how we do this, we shrink and swell the peds themselves, and that’s what changes the size of the macropores, slit spacings. But in a vertisol or in an actual soil, many of the peds don’t — I mean they change in size, but they stick together, and you get a larger crack that forms, that’s an accumulated width from all of the peds that are still stuck together. So you might get crack space, you know, a foot or two or three apart in the real world. But in the M&M model, these cracks are next to each ped. So that’s slightly different. And the idea is well, does this is still simulate what actually happens in a vertisol? And Professor Morgan at Texas A&M is testing this. So she’s in the process of finding out, applying the PALMS model, using the M&M, getting the characteristics for the soil, and modeling this to see if in fact, it does work in a vertisol. So we’re hopeful. But I think the jury’s still out.

LEO RIVERA 47:52
All right. Our next question is, can you obtain all of these parameters with a Guelph permeameter?

JOHN NORMAN 48:09
Well that’s a bit challenging. I haven’t actually thought about that. I mean, the Guelph permeameter does also use 3D flow. I think the challenge might be knowing the depths that you’re working at. In this sort of quasi one dimensional infiltration, we know that the water is going mainly down, and we can estimate to what depth the wetting front is getting. And so we know what depths that we’re working with in order to get, to use the saturated hydraulic conductivity to obtain this maximum head size. And with a Guelph permeameter, the geometry is different. And I would have to think about that for a while before I would be able to give you a confident answer on that. I think maybe that’s one I’d like to visit with Gaylon some on, and maybe we can put a more detailed answer into the record here for that question.

LEO RIVERA 49:18
All right, our next question, can you go back to the same location and repeat these measurements over time?

JOHN NORMAN 49:30
Yes, you can. The question is how long you wait. If you wait 30 minutes, I think you might get some very interesting information on the macropores slit width as a function of depth. But if you wait a week or two, you can go back. And in fact, I’ve done some experiments like this on compaction, where we made measurements of the ponded infiltration and then we compacted this soil under the sort of optimal moisture content for maximum compaction. And we compacted it at two pressures, at 10 pounds per square inch, and at 30 pounds per square inch, equivalent to a loaded combine and a tractor. And then, after we compacted those soils, we went back the next day and measured their infiltration rate again. And obviously it was much smaller. When you compact it, a lot of these macropores shut. And then each week following that, we would come back and measure the infiltration rates. And at 10 pounds per square inch, the saturated conductivity came back to its initial value within about three weeks. So the soil recovered quite quickly from the compaction at 10 pounds per square inch. At 30 pounds per square inch, the soil was at about half of the original saturated conductivity after about a month and a half. So it took, obviously took much longer to recover from the 30 pound per square inch compaction. And it turned out that the rate of recovery was directly proportional to the amount of residue that was on the surface. If the amount of residue on the surface was a full cover, the compaction was reversed much more quickly than if it was bare and there was no residue cover on the surface. So you can leave this ring in place and come back and make these measurements for weeks and weeks and weeks. And they seem to be very consistent. These measurements of saturated conductivity as a function of time following compaction increased in a very orderly way. Wasn’t a lot of random scatter in it, they just steadily increased. So I think you can do that.

LEO RIVERA 52:05
Alright, our next question, are there problems getting good measurements in sandy soil with very high K set?

JOHN NORMAN 52:20
Well, let’s see. We have measured pondered infiltration rates with this system with a seven inch head up to two meters an hour. Now, it takes two people to do those measurements because things are happening so fast, one person can’t keep up with it. But I think you could use this on a sand. I do believe that you can use this on a sand. We have lots of infiltration rates that are in the 500 to 1500 millimeters in our range. And and those are pretty high. They’re similar to what we get on the plainfield sand in central Wisconsin. We haven’t done this method on the plainfield sand, but we’ve used other methods, a much larger ring that was one meter by one meter in size. And we had a 300 gallon tank, and we used a method like that to measure that. So I think that this method, it is possible to do it on on the sand, how coarse a sand, we never have pushed that limit. But you can certainly work with saturated conductivities up into the 500, 700 millimeter per hour range, which is getting up there well into the sand range.

LEO RIVERA 54:00
All right. Our next question, do you need a macropore model for all soils, or do some soils not have macropores?

JOHN NORMAN 54:14
Some soils don’t have many macropores. I think that’s probably true. But in the soils that I’ve worked with, I would say maybe 10 or 15 soils of different textures across the state of Wisconsin. They all have macropores and maybe the reason for that is that they’re all moderately productive soils. So I guess my bias is that if a soil is relatively productive, that is if there’s vegetation growing on it and it has considerable vitality and is growing at a significant rate, it probably has macropores. So in the soils that I’ve seen that have very few macropores, not much grows on them. And so my suspicion is that these things are characteristic. When you get to the sand now, the sands, you know, are single grain structure, they’re not an aggregated structure. And so sands can be very productive, but they don’t hold much water as a result. If you don’t irrigate them, at least in Wisconsin, not much productivity comes from them. So at least on the agricultural side, my bias is is that any agricultural soil that is productive enough to be farmed is going to have lots of macropores. They provide the channels for the air to keep the soil aerated, and they establish an environment where the water holding capacity is greater and the infiltration capacity and water storage capacity is much greater than if those macropores are not there.

LEO RIVERA 56:08
All right. Our next question: according to your paper, “Measuring and modeling macroporous soil water and solute flux below the root zone of a plano silt-loam,” you use TDRs, and tensiometers, could you please compare methods described here against the ones described in your paper?

JOHN NORMAN 56:33
That paper was a PhD thesis of Brian Lepore. And that was an extraordinarily elaborate experiment. That was two years worth of work to do that experiment, and basically a huge number of TDRs to measure the moisture content and lysimeters buried at a meter depth and then saturating this whole system and measuring the drainage rate out of that system at a meter depth with large lysimeters, equilibrium tension lysimeters and looking at the time characteristics of the water content change and the drainage changes. So we could plot as a function of time how the drainage out of this block of soil that was about a meter by a meter by a meter deep, we could look at the time change and separate out the drainage that was associated with macropores and its volume from the drainage that was associated with mesopores from the drainage that was associated with micropores. So by monitoring the system for weeks after the saturated experiment, we had two methods for getting at the macropore characteristics. One was how the water content changed from the water content sensors. And the second one was the time sequence of drainage. And the two of them gave us a great deal of detailed information about the characteristics of the macropores. But those experiments were way more complicated, I think, than anyone’s going to want to do who wants to use a model and get some parameters in it. So what this, really this presentation has been about, has been a faster way, a practical way, of doing this on a farm field, for example, as I showed you, a practical way of getting the parameters for this macropore model. Now, we’re very encouraged by this because this same practical method we’re talking about here, we compared to that much more elegant, elaborate method that Brian Lepore used for his PhD. And they agree with each other very well. I mean, that really has encouraged us that at least on the soils that we’ve been working with, the silt loam soils, this simple method provides adequate parameterization for that macropore model. Good question.

LEO RIVERA 59:13
All right. Our next question: I’m not exactly sure what your macropore model does. For example, does it predict water flow through macropores not only when the water is ponded but also when there is a low suction head, say 10 centimeters or less?

JOHN NORMAN 59:36
Oh, let’s see, I have to do some quick calculations in my mind on that. It does deal with the flow of water through the macropores when the macropores are saturated, like they are in a ponded infiltration, as well as when they are unsaturated which is what occurs during rain events. So during rain events, the macropores are not full. Now, the size of the macropores we’re working with here typically are in the 100 micron range. These macropores are so large that a 10 centimeter suction, I don’t think there would be any water in these. I mean, I haven’t done that calculation quick in my head. But I think that with that suction, these macropores would all be empty. And so if you infiltrated with a 10 centimeter suction, say with a tension infiltrometer, then you would be infiltrating directly through the peds. And those infiltration rates would be, maybe of a factor of 10 to 1000 smaller than the ones we’re looking at here. So when the macropores are not activated, which happens at a pretty low tension, I mean, I think the tensions here are going to be on the order of the air entry potentials, basically, that by the time you get to the entry potentials and you’re on the moisture release curve, the macropores are probably mostly empty, in these soils, in the particular ones we’re working with. Some soils have smaller macropores, maybe in the range of 50 microns, or 30 or 50 microns, those soils may be conducting water at tensions of 10 centimeters of water, and then that would be part of the solution. So it kind of depends on the size of the macropores that you think that you’re working with. The methods I described here are an estimate or a way to estimate how